Задача Лагранжа с одним ограничением
Рассмотрим задачу, имеющую следующую структуру: f(X) ® max при условии (3) g(X) = 0. Рассмотрим пример. По склону горы идет дорога, требуется найти на ней самую высокую точку. На рис. 1 представлена карта местности с нанесенными на нее линиямиточку. На рис. 1 представлена карта местности с нанесенными на нее
линиями
 Рис. 1
равных высот; толстая линия – это дорога. Точка М, в которой дорога касается
одной линий уровня, - это и есть наивысшая точка дороги.
Если Х = (х1, х2) – точка плотности, х1 и х2 – её координаты, то задаче можно
придать следующую форму. Пусть f(Х) — высота точки Х над уровнем моря, а
уравнение g(X) = 0 описывает дорогу. Тогда наивысшая точка дороги - решение
задачи (3).
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой
высокой точкой местности, и ограничение можно было бы не принимать во
внимание.
Если же дорога не проходит через вершину, то, немного отклонившись от дороги,
можно было бы подняться выше, чем двигаясь строго по дороге. Отклонение от
дороги соответствует попаданию в такие точки, где g(X) ¹ 0; при
малых отклонениях достижимую при этом высоту можно приближенно считать
пропорциональной отклонению.
Идею решения задачи Лагранжа можно представить следующим образом: можно
попытаться "исправить” рельеф местности так, чтобы отклонение от дороги не
давало преимуществ в достижении высоты. Для этого нужно заменить высоту f(Х)
функцией.
L(X) = f(X) - lg(Х),
где множитель l подбирается таким образом, чтобы участок склона в окрестности
точки М стал горизонтальным (слишком малое l не устранит преимуществ
отклонений от дороги, а слишком большое – придаст преимущество отклонениям в
противоположную сторону).
Теперь, поскольку рельеф L(X) делает площадку в окрестности точки оптимума
горизонтальной, эта точка удовлетворяет равенствам
Рис. 1
равных высот; толстая линия – это дорога. Точка М, в которой дорога касается
одной линий уровня, - это и есть наивысшая точка дороги.
Если Х = (х1, х2) – точка плотности, х1 и х2 – её координаты, то задаче можно
придать следующую форму. Пусть f(Х) — высота точки Х над уровнем моря, а
уравнение g(X) = 0 описывает дорогу. Тогда наивысшая точка дороги - решение
задачи (3).
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой
высокой точкой местности, и ограничение можно было бы не принимать во
внимание.
Если же дорога не проходит через вершину, то, немного отклонившись от дороги,
можно было бы подняться выше, чем двигаясь строго по дороге. Отклонение от
дороги соответствует попаданию в такие точки, где g(X) ¹ 0; при
малых отклонениях достижимую при этом высоту можно приближенно считать
пропорциональной отклонению.
Идею решения задачи Лагранжа можно представить следующим образом: можно
попытаться "исправить” рельеф местности так, чтобы отклонение от дороги не
давало преимуществ в достижении высоты. Для этого нужно заменить высоту f(Х)
функцией.
L(X) = f(X) - lg(Х),
где множитель l подбирается таким образом, чтобы участок склона в окрестности
точки М стал горизонтальным (слишком малое l не устранит преимуществ
отклонений от дороги, а слишком большое – придаст преимущество отклонениям в
противоположную сторону).
Теперь, поскольку рельеф L(X) делает площадку в окрестности точки оптимума
горизонтальной, эта точка удовлетворяет равенствам
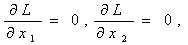 а так как точка лежит на дороге, то – и ограничению g(X) = 0.
рис.
а так как точка лежит на дороге, то – и ограничению g(X) = 0.
рис.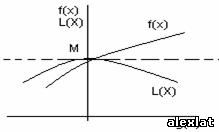 2
Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный
случай использован исключительно для наглядности. Подобным образом можно было
бы рассуждать и в общем, n-мерном случае.
Справедливо следующее утверждение:
Если f(х1,.,хn) и g(х1,.,хn) - непрерывно дифференцируемые функции всех своих
аргументов, то решение задачи
f(х1,.,хn) ® max
при условии
g(х1,.,хn) = 0
удовлетворяет равенствам 2
Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный
случай использован исключительно для наглядности. Подобным образом можно было
бы рассуждать и в общем, n-мерном случае.
Справедливо следующее утверждение:
Если f(х1,.,хn) и g(х1,.,хn) - непрерывно дифференцируемые функции всех своих
аргументов, то решение задачи
f(х1,.,хn) ® max
при условии
g(х1,.,хn) = 0
удовлетворяет равенствам
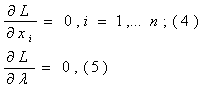 где
L(х1,.,хn;l) = f(х1,.,хn) — lg(х1,.,хn).
Функция L(X; l) получила название функции Лагранжа (или лагранжиана
) задачи (3), а коэффициент l — множителя Лагранжа.
Заметим, что равенство (5) — это представленное в другой форме ограничение
g(Х) = 0.
Приведенные выше рассуждения, разумеется, не являются доказательством
сформулированного здесь утверждения; они лишь помогают понять существо
метода: составляющая lg(Х) в составе функции Лагранжа должна уравновешивать
возможное увеличение максимального значения функции g(Х) от нуля. Это
обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла
множителя Лагранжа.
Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить
на берегу моря прямоугольный участок наибольшей площади (берег считается
прямолинейным).
Рис.3к
где
L(х1,.,хn;l) = f(х1,.,хn) — lg(х1,.,хn).
Функция L(X; l) получила название функции Лагранжа (или лагранжиана
) задачи (3), а коэффициент l — множителя Лагранжа.
Заметим, что равенство (5) — это представленное в другой форме ограничение
g(Х) = 0.
Приведенные выше рассуждения, разумеется, не являются доказательством
сформулированного здесь утверждения; они лишь помогают понять существо
метода: составляющая lg(Х) в составе функции Лагранжа должна уравновешивать
возможное увеличение максимального значения функции g(Х) от нуля. Это
обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла
множителя Лагранжа.
Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить
на берегу моря прямоугольный участок наибольшей площади (берег считается
прямолинейным).
Рис.3к 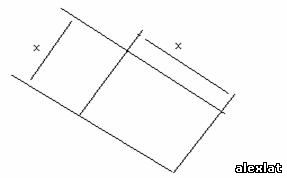 задаче Дидона
Обозначим стороны прямоугольника х1 и х2 (см. рис. 3). Решим сначала задачу
без использования метода Лагранжа.
Очевидно, х2 = А - 2 х1 и площадь прямоугольника равна
S = х1х2 = x1(А - 2х1). Рассматривая ее как функцию
одного аргумента х1, нетрудно найти его значение, при котором площадь
максимальна: х1 = А/4. Отсюда х2 = А/2. Максимальная площадь равна S* = А2
/8.
Теперь рассмотрим эту же задачу в форме задачи Лагранжа:
х1х2 ® max
при условии
2 х1 + х2 - А = 0
Лагранжиан этой задачи равен
L(х1,х2; l) = х1х2 - l(2х1 + х2 - А),
и условия экстремума имеют вид
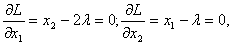 так что
х2 = 2l
х1 = l
2 х1 + х2 = А
Подставляя значения х1 и х2 из первого и второго равенств в третье, находим,
что 4l = А, откуда
l = А/4; х1 = А/4; х2 =А/2,
как и при решении первым способом.
Этот пример показывает распространенный способ решения задачи Лагранжа.
Соотношения (4) и (5) образуют систему уравнений относительно х1,.,хn и l,.
Система состоит из n + 1 уравнения - n уравнений вида (4) и одно уравнение
вида (5). Число уравнений равно числу неизвестных. Из уравнений вида (4)
можно попытаться выразить каждую из неизвестных х1,.,х2 через l, то есть
решить ее как систему из n уравнений, рассматривая l как параметр. Подставляя
получившиеся выражения в уравнение (5) – нам известно, что оно совпадает с
ограничением, - получаем уравнение относительно l. Решая его, находят l,
после чего определяются исходные неизвестные х1,.,хn.
так что
х2 = 2l
х1 = l
2 х1 + х2 = А
Подставляя значения х1 и х2 из первого и второго равенств в третье, находим,
что 4l = А, откуда
l = А/4; х1 = А/4; х2 =А/2,
как и при решении первым способом.
Этот пример показывает распространенный способ решения задачи Лагранжа.
Соотношения (4) и (5) образуют систему уравнений относительно х1,.,хn и l,.
Система состоит из n + 1 уравнения - n уравнений вида (4) и одно уравнение
вида (5). Число уравнений равно числу неизвестных. Из уравнений вида (4)
можно попытаться выразить каждую из неизвестных х1,.,х2 через l, то есть
решить ее как систему из n уравнений, рассматривая l как параметр. Подставляя
получившиеся выражения в уравнение (5) – нам известно, что оно совпадает с
ограничением, - получаем уравнение относительно l. Решая его, находят l,
после чего определяются исходные неизвестные х1,.,хn.
|  Рис. 1
равных высот; толстая линия – это дорога. Точка М, в которой дорога касается
одной линий уровня, - это и есть наивысшая точка дороги.
Если Х = (х1, х2) – точка плотности, х1 и х2 – её координаты, то задаче можно
придать следующую форму. Пусть f(Х) — высота точки Х над уровнем моря, а
уравнение g(X) = 0 описывает дорогу. Тогда наивысшая точка дороги - решение
задачи (3).
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой
высокой точкой местности, и ограничение можно было бы не принимать во
внимание.
Если же дорога не проходит через вершину, то, немного отклонившись от дороги,
можно было бы подняться выше, чем двигаясь строго по дороге. Отклонение от
дороги соответствует попаданию в такие точки, где g(X) ¹ 0; при
малых отклонениях достижимую при этом высоту можно приближенно считать
пропорциональной отклонению.
Идею решения задачи Лагранжа можно представить следующим образом: можно
попытаться "исправить” рельеф местности так, чтобы отклонение от дороги не
давало преимуществ в достижении высоты. Для этого нужно заменить высоту f(Х)
функцией.
L(X) = f(X) - lg(Х),
где множитель l подбирается таким образом, чтобы участок склона в окрестности
точки М стал горизонтальным (слишком малое l не устранит преимуществ
отклонений от дороги, а слишком большое – придаст преимущество отклонениям в
противоположную сторону).
Теперь, поскольку рельеф L(X) делает площадку в окрестности точки оптимума
горизонтальной, эта точка удовлетворяет равенствам
Рис. 1
равных высот; толстая линия – это дорога. Точка М, в которой дорога касается
одной линий уровня, - это и есть наивысшая точка дороги.
Если Х = (х1, х2) – точка плотности, х1 и х2 – её координаты, то задаче можно
придать следующую форму. Пусть f(Х) — высота точки Х над уровнем моря, а
уравнение g(X) = 0 описывает дорогу. Тогда наивысшая точка дороги - решение
задачи (3).
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой
высокой точкой местности, и ограничение можно было бы не принимать во
внимание.
Если же дорога не проходит через вершину, то, немного отклонившись от дороги,
можно было бы подняться выше, чем двигаясь строго по дороге. Отклонение от
дороги соответствует попаданию в такие точки, где g(X) ¹ 0; при
малых отклонениях достижимую при этом высоту можно приближенно считать
пропорциональной отклонению.
Идею решения задачи Лагранжа можно представить следующим образом: можно
попытаться "исправить” рельеф местности так, чтобы отклонение от дороги не
давало преимуществ в достижении высоты. Для этого нужно заменить высоту f(Х)
функцией.
L(X) = f(X) - lg(Х),
где множитель l подбирается таким образом, чтобы участок склона в окрестности
точки М стал горизонтальным (слишком малое l не устранит преимуществ
отклонений от дороги, а слишком большое – придаст преимущество отклонениям в
противоположную сторону).
Теперь, поскольку рельеф L(X) делает площадку в окрестности точки оптимума
горизонтальной, эта точка удовлетворяет равенствам
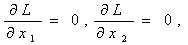 а так как точка лежит на дороге, то – и ограничению g(X) = 0.
рис.
а так как точка лежит на дороге, то – и ограничению g(X) = 0.
рис. 2
Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный
случай использован исключительно для наглядности. Подобным образом можно было
бы рассуждать и в общем, n-мерном случае.
Справедливо следующее утверждение:
Если f(х1,.,хn) и g(х1,.,хn) - непрерывно дифференцируемые функции всех своих
аргументов, то решение задачи
f(х1,.,хn) ® max
при условии
g(х1,.,хn) = 0
удовлетворяет равенствам
2
Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный
случай использован исключительно для наглядности. Подобным образом можно было
бы рассуждать и в общем, n-мерном случае.
Справедливо следующее утверждение:
Если f(х1,.,хn) и g(х1,.,хn) - непрерывно дифференцируемые функции всех своих
аргументов, то решение задачи
f(х1,.,хn) ® max
при условии
g(х1,.,хn) = 0
удовлетворяет равенствам
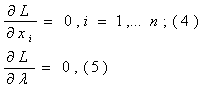 где
L(х1,.,хn;l) = f(х1,.,хn) — lg(х1,.,хn).
Функция L(X; l) получила название функции Лагранжа (или лагранжиана
) задачи (3), а коэффициент l — множителя Лагранжа.
Заметим, что равенство (5) — это представленное в другой форме ограничение
g(Х) = 0.
Приведенные выше рассуждения, разумеется, не являются доказательством
сформулированного здесь утверждения; они лишь помогают понять существо
метода: составляющая lg(Х) в составе функции Лагранжа должна уравновешивать
возможное увеличение максимального значения функции g(Х) от нуля. Это
обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла
множителя Лагранжа.
Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить
на берегу моря прямоугольный участок наибольшей площади (берег считается
прямолинейным).
Рис.3к
где
L(х1,.,хn;l) = f(х1,.,хn) — lg(х1,.,хn).
Функция L(X; l) получила название функции Лагранжа (или лагранжиана
) задачи (3), а коэффициент l — множителя Лагранжа.
Заметим, что равенство (5) — это представленное в другой форме ограничение
g(Х) = 0.
Приведенные выше рассуждения, разумеется, не являются доказательством
сформулированного здесь утверждения; они лишь помогают понять существо
метода: составляющая lg(Х) в составе функции Лагранжа должна уравновешивать
возможное увеличение максимального значения функции g(Х) от нуля. Это
обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла
множителя Лагранжа.
Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить
на берегу моря прямоугольный участок наибольшей площади (берег считается
прямолинейным).
Рис.3к 
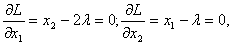 так что
х2 = 2l
х1 = l
2 х1 + х2 = А
Подставляя значения х1 и х2 из первого и второго равенств в третье, находим,
что 4l = А, откуда
l = А/4; х1 = А/4; х2 =А/2,
как и при решении первым способом.
Этот пример показывает распространенный способ решения задачи Лагранжа.
Соотношения (4) и (5) образуют систему уравнений относительно х1,.,хn и l,.
Система состоит из n + 1 уравнения - n уравнений вида (4) и одно уравнение
вида (5). Число уравнений равно числу неизвестных. Из уравнений вида (4)
можно попытаться выразить каждую из неизвестных х1,.,х2 через l, то есть
решить ее как систему из n уравнений, рассматривая l как параметр. Подставляя
получившиеся выражения в уравнение (5) – нам известно, что оно совпадает с
ограничением, - получаем уравнение относительно l. Решая его, находят l,
после чего определяются исходные неизвестные х1,.,хn.
так что
х2 = 2l
х1 = l
2 х1 + х2 = А
Подставляя значения х1 и х2 из первого и второго равенств в третье, находим,
что 4l = А, откуда
l = А/4; х1 = А/4; х2 =А/2,
как и при решении первым способом.
Этот пример показывает распространенный способ решения задачи Лагранжа.
Соотношения (4) и (5) образуют систему уравнений относительно х1,.,хn и l,.
Система состоит из n + 1 уравнения - n уравнений вида (4) и одно уравнение
вида (5). Число уравнений равно числу неизвестных. Из уравнений вида (4)
можно попытаться выразить каждую из неизвестных х1,.,х2 через l, то есть
решить ее как систему из n уравнений, рассматривая l как параметр. Подставляя
получившиеся выражения в уравнение (5) – нам известно, что оно совпадает с
ограничением, - получаем уравнение относительно l. Решая его, находят l,
после чего определяются исходные неизвестные х1,.,хn.