| Главная » Файлы » Сканави_ Сборник задач по математике |
| В разделе материалов: 3867 Показано материалов: 3601-3620 |
Страницы: « 1 2 ... 179 180 181 182 183 ... 193 194 » |
|
ⁿ√2+√3 + ⁿ√2 - √3 ˃2  |
|
Без помощи таблиц показать, что 2 < log32 + log23 < 3 |
|
Доказать что,если (x²+ 5x + 6) (x² +11x + 30) < 0 то sin2x > 0 |
|
Числа x1 и x2 являются действительными корнями уравнений, 5x³ - 6 = 0 и 6x³- 5 = 0 соответственно. Показать,что x1+x2 >2 |
|
log ₂ ( χ -1) - log ₂( χ +1) + log χ₊₁/χ₋₁ 2 ˃ 0 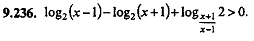 |
|
log χ log ₂ ( 4 χ -12 ) ≤ 1 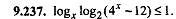 |
|
10 ∙ 0,3∜log 1/√3(tg χ ) > 3 |
|
2 ˂ 2( sinχ/1- cosχ )² ˂ 8 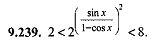 |
|
Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 3, 5, 7, если каждое число не должно содержать одинаковых цифр?
Комбинаторика,Бином Ньютона и Комплексные числа |
Просмотров: 796 |
Загрузок: 0 |
|
Дата: 25.11.2013
| Комментарии (0)
|
|
3 ∙ 2 cos ² χ - 6 / 2 cos ² χ - 1 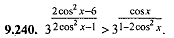 |
|
0,2 cos 2 χ - 1 / 25 cos 2 χ ˂ 4 ∙ 125 ⁻ ½ 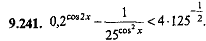 |
|
log χ log 3 ( 9 ˣ - 6 ) ≥ 1 |
|
log ₁/₂ ( χ² + 4χ) ˂1( χ ϵ Z )  |
|
Решить неравенства √1- 9 ∙ (log ⅛ χ )² >1-4 ∙ log ⅛ χ |
|
Решить неравенства log ½ χ+√1- 4(log ½ χ ) ² < 1 |
|
logx²(3 - 2x) > 1 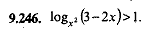 |
|
Решить неравенства log 3(4ˣ + 1 ) + log4ˣ+1 3 >2,5 |
|
Решить неравенства log3(3ˣ - 1) ∙ log⅓ ( 3ˣ⁺² - 9)> -3 |
|
Решить неравенства log ρ 1+ log² ρ χ / 1- log ρ χ < 0 |
|
На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом?
Комбинаторика,Бином Ньютона и Комплексные числа |
Просмотров: 603 |
Загрузок: 0 |
|
Дата: 25.11.2013
| Комментарии (0)
|
Категории раздела
| Алгебра [52] |
| Тождество [503] |
| Прогрессии [53] |
| Координаты и Вектороы [35] |
| Алгебраические уравнения [250] |
| Логарифмы [348] |
| Тригонометрические уравнения [499] |
| Неравенства [305] |
| Задачи по планиметрии [433] |
| Задачи стереометрии [234] |
| Задачи по Геометрии с применением Тригонометрии [450] |
| Применение уравнений к решению задач [453] |
| Математический Анализ [60] |
| Комбинаторика,Бином Ньютона и Комплексные числа [80] |
| Элементарная математика [112] |
Друзья сайта