| Главная » Файлы » Сканави_ Сборник задач по математике » Неравенства |
| В категории материалов: 305 Показано материалов: 201-220 |
Страницы: « 1 2 ... 9 10 11 12 13 ... 15 16 » |
Сортировать по: Дате · Названию · Рейтингу · Комментариям · Загрузкам · Просмотрам
|
Доказать,что из всех прямоугольных параллелепипедов с данной суммой всех ребер наибольший объем имеет куб.(Для доказательства можно использовать, например, неравенство α + b + c + d / 2 ≥∜αbcd, верное для всяких положительных чисе |
|
При каких значениях Р система неравенств -9 < 3 χ² + ρχ-6/ χ² - χ+1< 6 выполняется всеми действительными значениями х? |
|
(x - 1) · lg + lg(2x + 1+1) < lg(7 · 2x+12) log x(x + 2) > 2 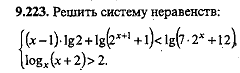 |
|
γ = √ sin x - 0,5 + log ₃ ( 25 - χ² )  |
|
γ = √ sin x - 0,5 + log ₃ ( 25 - χ² )  |
|
Доказать,что при а > 0, b > 0, с > 0 и d > 0 справедливо неравенство α + b + c + d /4 ≥ ∜ αbcd |
|
При каких значениях m неравенство - 6 ˂ 2χ ² + mχ - 4 / χ ² - χ +1 ˂ 14 выполняется для всех действительных значений χ? |
|
(1+γ/χ )(1+z/γ )( 1+χ/z) ≥ 8 ( χ ˃0, γ ˃0 ,z ˃0)  |
|
α³+b³/2 ≥ ( α+b/2)³ ( α ˃ 0,b ˃ 0 )  |
|
α ⁴+ b ⁴ /2 ≥ ( α + b/2) ⁴  |
|
ⁿ√2+√3 + ⁿ√2 - √3 ˃2  |
|
Без помощи таблиц показать, что 2 < log32 + log23 < 3 |
|
Доказать что,если (x²+ 5x + 6) (x² +11x + 30) < 0 то sin2x > 0 |
|
Числа x1 и x2 являются действительными корнями уравнений, 5x³ - 6 = 0 и 6x³- 5 = 0 соответственно. Показать,что x1+x2 >2 |
|
log ₂ ( χ -1) - log ₂( χ +1) + log χ₊₁/χ₋₁ 2 ˃ 0 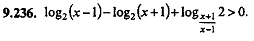 |
|
log χ log ₂ ( 4 χ -12 ) ≤ 1 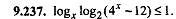 |
|
10 ∙ 0,3∜log 1/√3(tg χ ) > 3 |
|
2 ˂ 2( sinχ/1- cosχ )² ˂ 8 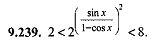 |
|
3 ∙ 2 cos ² χ - 6 / 2 cos ² χ - 1 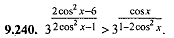 |
|
0,2 cos 2 χ - 1 / 25 cos 2 χ ˂ 4 ∙ 125 ⁻ ½ 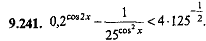 |
Категории раздела
| Алгебра [52] |
| Тождество [503] |
| Прогрессии [53] |
| Координаты и Вектороы [35] |
| Алгебраические уравнения [250] |
| Логарифмы [348] |
| Тригонометрические уравнения [499] |
| Неравенства [305] |
| Задачи по планиметрии [433] |
| Задачи стереометрии [234] |
| Задачи по Геометрии с применением Тригонометрии [450] |
| Применение уравнений к решению задач [453] |
| Математический Анализ [60] |
| Комбинаторика,Бином Ньютона и Комплексные числа [80] |
| Элементарная математика [112] |
Друзья сайта