Сканави_ Сборник задач по математике - Каталог файлов

Главная » Файлы » Сканави_ Сборник задач по математике

В разделе материалов: 3867
Показано материалов: 2181-2200

Страницы: « 1 2 ... 108 109 110 111 112 ... 193 194 »

3.487_ Зная,что sin (5π/2-χ)3/5, найти sinχ/2 sin5χ/2

Зная,что sin (5π/2-χ)3/5,
найти
sinχ/2 sin5χ/2

3.488_ (1 -sinα)(1-sinβ)(1-sinγ)=(1+sinα)(1+sinβ)(1+sinγ)

Доказать,что если для некоторых чисел α,β и γ выполняется равенство (1 -sinα)(1-sinβ)(1-sinγ)=(1+sinα)(1+sinβ)(1+sinγ),то тогда каждая из частей этого равенство равна |cosαcosβcosγ|

3.489_1- tgφ + tg²φ- tg³φ +...=

Доказать,что для чисел φ удовлетворяющих неравенствам 0 <φ <π/4,
выполняется равенство
1- tgφ + tg²φ- tg³φ +...=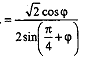

3.490_Найти наименьшее значение выражения sin⁶α+cos⁶α

Найти наименьшее значение выражения
sin⁶α+cos⁶α при 0 ≤ α ≤π/2

3.491_Найти наименьшее значение выражения sin⁴α+cos⁴α

Найти наименьшее значение выражения
sin⁴α+cos⁴α при 0 ≤ α ≤π/2

3.492_ƒ(χ)=cos²χ+cos²(α+χ)-2cosαcosχcos(α+χ)

Показать,что если постоянно,то функция
ƒ(χ)=cos²χ+cos²(α+χ)-2cosαcosχcos(α+χ) также является постоянной.

3.493_Найти сумму 1+cos4α+cos8α+...+cos4nα

Найти сумму 1+cos4α+cos8α+...+cos4nα

3.494_Показать,что если χ = tg5°,γ = tg20°

Показать,что если χ = tg5°,γ = tg20° и z = tg65° то χγ+γz+zχ =1

3.495_Доказать,что tg142°30°+√ 6+√ 3 -√2

Доказать,что tg142°30°+√ 6+√ 3 -√2—есть целое число.

3.496_Доказать,что 8sinA/2sinB/2sinC/2 ≤1

Пусть A,B,C —углы треугольника. Доказать,что 8sinA/2sinB/2sinC/2 ≤1

3.497_arctgχ+arctgγ+arctgz = π

Показать,что если arctgχ+arctgγ+arctgz = π
то χ+γ+z = χγz

3.498_Показать,что если arctgχ+arctgγ +arctgz = π/2

Показать,что если arctgχ+arctgγ +arctgz = π/2
то
χγ+γz+zχ =1

3.499_ Доказать,что 8cosAcosBcosC≤1

Пусть A,B,C—углы треугольника. Доказать,что 8cosAcosBcosC≤1

3.500_sin²A+sin²B+sin²C ≤ 9/4

ПустьA,B,C— углы треугольника.
Используя неравенство cosAcosBcosC≤1/8 доказать,что
sin²A+sin²B+sin²C ≤ 9/4

3√x +3√x - 1 - 3√x - 2 < 11

3^√x +3^{√x - 1} - 3^{√x - 2} < 11

3ху —x2 — y2 < 7

Доказать, что при условии
2у + 5х = 10 выполняется неравенство

3ху —x² — y² < 7.

4,081_Найти произведение n первых членов геометрической прогрессии

Найти произведение n первых членов геометрической прогрессии, если известна их сумма s и сумма δ из обратных величин

4.001_За установку самого нижнего железобетонного кольца

За установку самого нижнего железобетонного кольца заплатили 2600 руб. а за каждое следующее заплатили 200 руб. меньше чем за предыдущее . Кроме такого,по окончании работы было уплачено еще 4000 руб.
Средная стоимость изготовления и установки одного кольца оказалась равной 2244 1/9 руб.
Сколько колец было установлено?

4.002_Сумма первого и пятого членов арифметической прогрессии

Сумма первого и пятого членов арифметической прогрессии равна 5/3 а произведение третьего и четвертого ее членов равна 65/72. Найти сумму 17 первых членов этой прогрессии

4.003_В соревновании по стрельбе за каждый промах

В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки за первый промах - одно штрафное очко, а за каждый последующий -на 1/2 очка больше,чем за предыдущий Сколько раз попал в цель стрелок,получивший 7 штрафных очков