| Главная » Файлы » Сканави_ Сборник задач по математике |
| В разделе материалов: 3867 Показано материалов: 601-620 |
Страницы: « 1 2 ... 29 30 31 32 33 ... 193 194 » |
|
Основанием прямого параллелепипеда служит ромб, площадь которого равна Q,площади диагональных сечений равны S1 и S2  |
|
Боковое ребро правильной четырехугольной пирамиды равно l и наклонено к плоскости основания под углом 60° 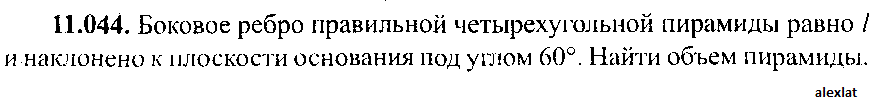 |
|
Наибольшая диагональ правильной шестиугольной призмы равна d и составляет с боковым ребром призмы угол 30°  |
|
Стороны основания прямоугольного параллелепипеда равны а и b. Диагональ параллелепипеда наклонена к боковой грани, содержащей сторону основания, равную b, под углом 30°  |
|
Стороны основания прямоугольного параллелепипеда равны а и b. Диагональ параллелепипеда наклонена к плоскости основания под углом 60°. Определить боковую поверхность параллелепипеда  |
|
Найти объем наклонной треугольной призмы, основанием которой служит равносторонний треугольник со стороной, равной а, если боковое ребро призмы равно стороне основания и наклонено к плоскости основания под углом 60°.  |
|
Найти объем правильной треугольной призмы, если сторoна ее основания равна a и боковая поверхность равновелика сумме оснований.  |
|
Найти боковую поверхность правильной шестиугольной пирамиды, высота которой равна h, а боковое ребро равно l 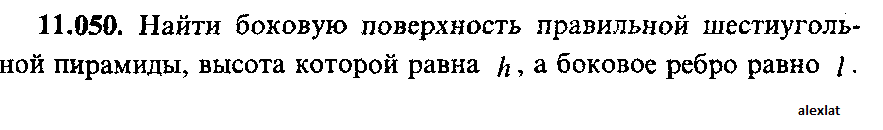 |
|
Найти объем правильной треугольной пирамиды у которой угол при вершине равен 90° 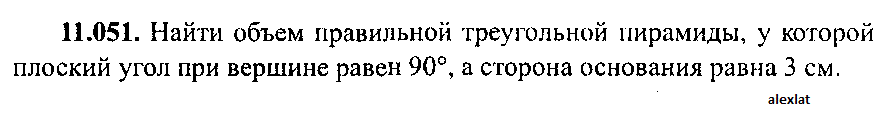 |
|
В правильной треугольной призме площадь сечения проходящего через боковое ребро равно Q  |
|
Высота правильного тетраэдра равна h. Вычислить его полную поверхность  |
|
Каждое из боковых ребер пирамиды равно b. Ее основанием служит прямоугольный треугольник, катеты которого относятся, как m : n, а гипотенуза равна с. Вычислить объем пирамиды.  |
|
Центр верхнего основания куба соединен с серединами сторон нижнего основания. Образовался четырёхгранный угол,каждый плоский угол которого равен a. Доказать что 30°< a <45°  |
|
Диагональ прямоугольного параллелепипеда равна 10 см.и образует с плоскостью основания угол 60°  |
|
Определить объем прямоугольного параллелепипеда, если его диагональ равна d, а длина ребер относится, как m : n : р.  |
|
Определить объем правильной треугольной пирамиды, если высота треугольника, служащего ее основанием, равна h, а апофема пирамиды равна m.  |
|
Площади боковых граней прямой треугольной призмы равны M, N и P боковое ребро равно l  |
|
Известны площадь основания P и объем V правильной четырехугольной призмы  |
|
Найти боковую поверхность правильной треугольной призмы с высотой h, если прямая, соединяющая центр верхнего основания с серединой стороны нижнего основания, наклонена к плоскости под углом 60°  |
|
В основании пирамиды лежит квадрат. Две боковые грани ее перпендикулярны к плоскости основания, а две другие наклонены к нему под углом в 45°. Среднее по величине боковое ребро равно l . Найти объем и полную поверхность пирамиды  |
Категории раздела
| Алгебра [52] |
| Тождество [503] |
| Прогрессии [53] |
| Координаты и Вектороы [35] |
| Алгебраические уравнения [250] |
| Логарифмы [348] |
| Тригонометрические уравнения [499] |
| Неравенства [305] |
| Задачи по планиметрии [433] |
| Задачи стереометрии [234] |
| Задачи по Геометрии с применением Тригонометрии [450] |
| Применение уравнений к решению задач [453] |
| Математический Анализ [60] |
| Комбинаторика,Бином Ньютона и Комплексные числа [80] |
| Элементарная математика [112] |
Друзья сайта