Сканави_ Сборник задач по математике - Каталог файлов

Главная » Файлы » Сканави_ Сборник задач по математике

В разделе материалов: 3867
Показано материалов: 581-600

Страницы: « 1 2 ... 28 29 30 31 32 ... 193 194 »

11.023 _ В правильной четырехугольной пирамиде сторона основания 6 дм

В правильной четырехугольной пирамиде сторона основания 6 дм, а высота 4 дм

11.024_ Основаниями правильной усеченной пирамиды

Основаниями правильной усеченной пирамиды служат квадраты со сторонами а и b (a > b). Боковые ребра наклонены к плоскости основания под углом 45°. Определить объем усеченной пирамиды

11.025_Боковые ребра правильной усеченной треугольной пирамиды

Боковые ребра правильной усеченной треугольной пирамиды наклонены к плоскости основания 60°

11.026_ Основанием прямого параллелепипеда служит ромб

Основанием прямого параллелепипеда служит ромб. Плоскость, проведённая через одну из сторон нижнего основания и противоположную сторону верхнего основания, образует с плоскостью основания угол 45°

11.027_ Определить объем правильной четырехугольной пирамиды

Определить объем правильной четырехугольной пирамиды, если ее боковое ребро составляет с плоскостью основания угол 45°, а площадь диагонального сечения равна S

11.028_ Основанием пирамиды служит ромб с острым углом 30°.

Основанием пирамиды служит ромб с острым углом 30°. Боковые грани наклонены к плоскости основания под углом 60°. Определить объем и полную поверхность пирамиды, если радиус вписанного в ромб круга равен r.

11.029_ Объем правильной треугольной пирамиды

Объем правильной треугольной пирамиды, боковая грань которой наклонена к плоскостью основания под углом 45°,равен 9 см³

11.030_ В основании прямого параллелепипеда лежит параллелограмм

В основании прямого параллелепипеда лежит параллелограмм со сторонами 1 и 4 и острым углом 60° градусов. Большая диагональ параллелепипеда равна 5. Определить его объём

11.031_ Центр куба, ребро которого равно а, соединен со всеми его вершинами

Центр куба, ребро которого равно а, соединен со всеми его вершинами. Определить объем и поверхность каждой из образовавшихся пирамид.

11.032_Основание пирамиды — равнобедренный треугольник

Основание пирамиды — равнобедренный треугольник с основанием 6 и высотой 9. Каждое боковое ребро равно 13. Найдите объём пирамиды

11.033_В треугольной пирамиде боковые ребра взаимно перпендикулярны

В треугольной пирамиде боковые ребра взаимно перпендикулярны и имеют длины √70 , √99 и √126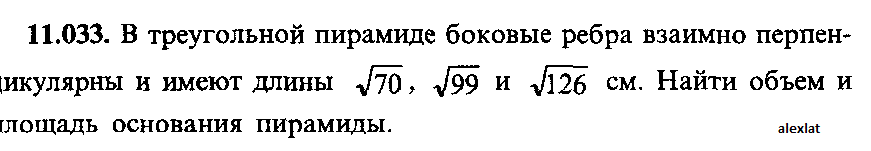

11.034_ Определить объем правильной шестиугольной призмы

Определить объем правильной шестиугольной призмы, у которой наибольшая диагональ равна d, а боковые грани квадраты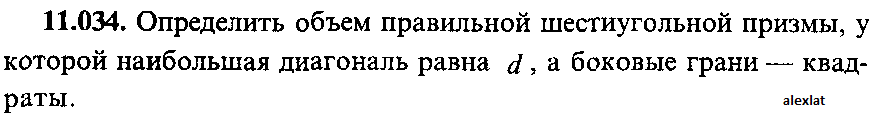

11.035 _ Найти объем куба если расстояние от его диагонали

Найти объем куба, если расстояние от его диагонали до непересекающегося с ней ребра равно d.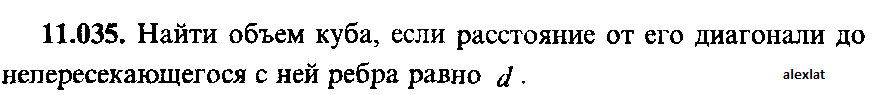

11.036_Определить объем октаэдра , ребро которого равно а

Определить объем октаэдра (правильного восьмигранника), ребро которого равно а

11.037_ Основание призмы - квадрат со стороной, равной а

Основание призмы — квадрат со стороной, равной а. Одна из боковых граней — тоже квадрат, другая — ромб, с углом в 60°

11.038_Основанием параллелепипеда служит квадрат.

Основанием параллелепипеда служит квадрат. Одна из вершин верхнего основания равноудалена от всех вершин нижнего основания и находится на расстоянии b от этого основания.

11.039_ В кубе центры оснований соединены с центрами боковых граней

В кубе центры оснований соединены с центрами боковых граней. Вычислить поверхность получившегося октаэдра, если ребро куба равно а

11.040_ Основанием пирамиды служит треугольник с длинами сторон 6 см

Основанием пирамиды служит треугольник с длинами сторон 6 см, 5 см и 5 см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по 45°