| Главная » Файлы » Сканави_ Сборник задач по математике » Задачи стереометрии |
| В категории материалов: 234 Показано материалов: 161-180 |
Страницы: « 1 2 ... 7 8 9 10 11 12 » |
Сортировать по: Дате · Названию · Рейтингу · Комментариям · Загрузкам · Просмотрам
|
В треугольной пирамиде две боковые грани взаимно перпендикулярны. Площади этих граней равны Р и Q, а длина их общего ребра равна а. Определить объем пирамиды. |
|
В треугольной пирамиде все четыре грани — равные равнобедренные треугольники с основанием, равным а, и боковой стороной, равной b. Вычислить объем пирамиды. При всяких ли а и b задача имеет решение? |
|
В наклонной треугольной призме расстояния боковых ребер друг от друга равны а, b и с. Бокозое ребро равно l , высота призмы равна h. Определить полную поверхность призмы |
|
Сторона основания правильной треугольной призмы меньше бокового ребра и равна а. Через сторону верхнего основания проведена плоскость, которая составляет с плоскостью основания угол в 45° и делит призму на две части. Определить объем и полную поверхность верхней части призмы. |
|
Диагонали граней прямоугольного параллелепипеда равны а, b и с. Определить его полную поверхность. |
|
Длины ребер параллелепипеда равны а, b и с. Ребра, длины которых равны а и b, взаимно перпендикулярны, а ребро длиной с образует с каждым из них угол в 60°. Определить объем параллелепипеда. |
|
Основанием прямого параллелепипеда служит параллелограмм с углом в 120° и сторонами, равными 3 см и 4 см. Меньшая диагональ параллелепипеда равна большей диагонали основания. Найти объем параллелепипеда. |
|
Основанем пирамиды служит прямоугольник, площадь которого равна S. Две боковые грани перпендикулярны к плоскости основания, а две другие наклонены к ней под углами в 30° и 60°. Найти объем пирамиды. |
|
Через вершину основания и середины двух боковых ребер правильной треугольной пирамиды проведена плоскость. Найти отношение боковой поверхности пирамиды к площади ее основания, если известно, что секущая плоскость перпендикулярна к боковой грани. |
|
Из середины высоты правильной треугольной пирамиды опущены перпендикуляры на боковое ребро и на боковую грань. Длины этих перпендикуляров соответственно равны а и b. Найти объем пирамиды. При всяких ли а и b задача имеет решение? |
|
В полушар радиуса R вписан куб так, что четыре его вершины лежат на основании полушара, а другие четыре вершины расположены на его сферической поверхности. Вычислить объем куба. |
|
Угол между образующей конуса и плоскостью основания равен 30°. Боковая поверхность конуса равна 3π√3 ед2. Определить объем правильной шестиугольной пирамиды, вписанной в этот конус. |
|
Около шара радиуса R описана правильная шестиугольная призма. Определить ее полную поверхность |
|
В шар радиуса R вписана правильная шестиугольная усеченная пирамида, у которой плоскость нижнего основания проходит через центр шара, а боковое ребро составляет с плоскостью основания угол в 60°. Определить объем пирамиды. |
|
Около шара описан прямой параллелепипед, у которого диагонали основания равны а и b. Определить полную поверхность этого параллелепипеда. |
|
В шар радиуса R вписана правильная четырехугольная пирамида. Определить объем этой пирамиды, если радиус окружности, описанной вокруг ее основания, равен r. |
|
Конус образован вращением прямоугольного треугольника площади S вокруг одного из катетов. Найти объем конуса, если длина окружности, описанной при вращении этого треугольника точкой пересечения его медиан, равна L. |
|
Треугольник со сторонами, равными а, b и с, вращается поочередно около каждой из своих сторон. Найти отношение объемов получающихся при этом тел. |
|
Дан куб ABCDA1B1C1D1, ребро которого равно a 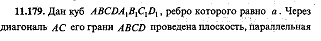 |
|
На ребре двугранного угла 120 ° взят отрезок длиной c  |
Категории раздела
| Алгебра [52] |
| Тождество [503] |
| Прогрессии [53] |
| Координаты и Вектороы [35] |
| Алгебраические уравнения [250] |
| Логарифмы [348] |
| Тригонометрические уравнения [499] |
| Неравенства [305] |
| Задачи по планиметрии [433] |
| Задачи стереометрии [234] |
| Задачи по Геометрии с применением Тригонометрии [450] |
| Применение уравнений к решению задач [453] |
| Математический Анализ [60] |
| Комбинаторика,Бином Ньютона и Комплексные числа [80] |
| Элементарная математика [112] |
Друзья сайта