| Главная » Файлы » Сканави_ Сборник задач по математике |
| В разделе материалов: 3867 Показано материалов: 361-380 |
Страницы: « 1 2 ... 17 18 19 20 21 ... 193 194 » |
|
Показать, что во всяком прямоугольном треугольнике сумма полупериметра и радиуса вписанной окружности равна сумме катетов. 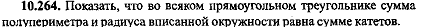 |
|
Показать, что во всяком прямоугольном треугольнике сумма полупериметра и радиуса вписанной окружности равна сумме катетов 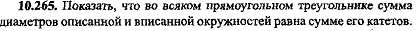 |
|
Найти третью сторону остроугольного треугольника, если две стороны остроугольного треугольника равны а и b.  |
|
На отрезке AB взята точка C и на частях AC и CB отрезка AB  |
|
Точка C перемещается по отрезке AB длиной l  |
|
Высоты треугольника равны 12, 15 и 20 см. Доказать, что треугольник прямо угольный 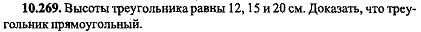 |
|
Возвести в степень (√2(cos5π/18+i sin5π/18))⁶
Комбинаторика,Бином Ньютона и Комплексные числа |
Просмотров: 681 |
Загрузок: 0 |
|
Дата: 29.11.2013
| Комментарии (0)
|
|
Найдите отношение суммы квадратов всех медиан треугольника к сумме квадратов сторон 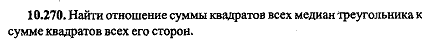 |
|
Найти площадь треугольника,если его высоты равны 10,15 и 20 см  |
|
Числа m1, m2 и m3 выражают длины медиан некоторого треугольника  |
|
Высота,проведенная гипотенузе прямоугольного треугольника, делит его 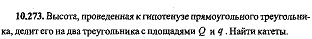 |
|
Числа h1,h2 и h3 выражают длины высот некоторого треугольника 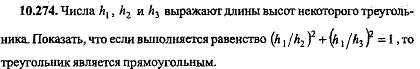 |
|
Через точку пересечения диагоналей трапеции параллельно основаниям 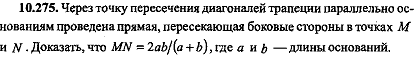 |
|
Найти биссектрису угла треугоьника, у которого катеты равны a и b 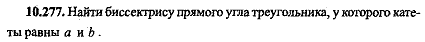 |
|
Дан квадрат, сторона которого равна а. Определить стороны равновеликого ему равнобедренного треугольника, у которого сумма длин основания и высоты, опущенной на основание, равна сумме длин двух боковых сторон  |
|
Точки M, N,P,Q являются серединами сторон AB, BC, CD и DA ромба ABCD
 |
|
Возвести в степень (-1+√3i)⁹
Комбинаторика,Бином Ньютона и Комплексные числа |
Просмотров: 837 |
Загрузок: 0 |
|
Дата: 29.11.2013
| Комментарии (0)
|
|
Определить углы равнобедренного треугольника,если его площадь относится 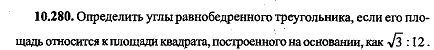 |
|
В окружность вписан четырехугольник с углами 120 ° ,90 ° ,60 ° и 90 °  |
|
В треугольнике ABC проведена прямая DE, параллельная основанию AC. Площадь треугольника ABC равна 8, а площадь треугольника DEC равна 2. Найдите отношение отрезка DE к основанию треугольника ABC.  |
Категории раздела
| Алгебра [52] |
| Тождество [503] |
| Прогрессии [53] |
| Координаты и Вектороы [35] |
| Алгебраические уравнения [250] |
| Логарифмы [348] |
| Тригонометрические уравнения [499] |
| Неравенства [305] |
| Задачи по планиметрии [433] |
| Задачи стереометрии [234] |
| Задачи по Геометрии с применением Тригонометрии [450] |
| Применение уравнений к решению задач [453] |
| Математический Анализ [60] |
| Комбинаторика,Бином Ньютона и Комплексные числа [80] |
| Элементарная математика [112] |
Друзья сайта