| Главная » Файлы » Математика » Функция и Графики |
| 28.10.2013, 00:58 | |
| Построить график функции y = |x ² - 2x| График функции y = f(x) + g(x) 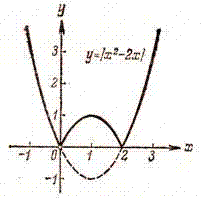 График этой функции - парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х2—2х|, исходя из графика функции у = х2 — 2x
График функции y = f(x) + g(x) Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x). Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x). Пусть точки (х0, y1) и (х0, у2) соответственно принадлежат графикам функций y = f{x) и y = g(х), т. е. y1 = f(x0), y2 = g(х0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х0) + g(x0) = y1 +y2),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x). и y = g(х) заменой каждой точки (хn, у1) графика функции y = f(x) точкой (хn, y1 + y2), где у2 = g(xn), т. е. сдвигом каждой точки (хn, у1) графика функцииy = f(x) вдоль оси у на величину y1 = g(хn). При этом рассматриваются только такие точки хn для которых определены обе функции y = f(x) и y = g(x). Такой метод построения графика функции y = f(x) + g(х) называется сложением графиков функций y = f(x) и y = g(x)
| |
| Просмотров: 1094 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |