| Главная » Файлы » Математика » Теория графов |
| В категории материалов: 47 Показано материалов: 1-20 |
Страницы: 1 2 3 » |
Сортировать по: Дате · Названию · Рейтингу · Комментариям · Загрузкам · Просмотрам
|
На рис. 2 изображен неориентированный граф G = (X, A). |
|
На рис. 3 изображен ориентированный граф G = (X, A). |
|
На рис. 4. изображен ориентированный граф G = (X, A). |
|
В графе, изображенном на рис. 2, концами ребра a1 являются вершины x1, x2; вершина x2 инцидентна ребрам a1, a2; |
|
В изображенном на рис. 8 графе рассмотрим два маршрута из вершины x1 в вершину x4: |
|
В приведенном на рис. 9 графе выделим следующие маршруты: (a1,a3,a4) – простая элементарная цепь длины 3, т.к. все ребра и вершины попарно различны; |
|
В приведенном на рис. 10. графе выделим следующие пути: (x1,x2,x3,x4) – простой элементарный путь, т.к. каждая вершина и каждая дуга используются не более одного раза; |
|
Граф G' = ({1, 2, 3}; |
|
Графы, изображенные на рис. 1.18, являются деревьями. |
|
Дана матрица 1 0 2 0 0 2 0 0 1 0 3 1 0 0 1 4 3 1 0 0 1 2 3 4 Постройте орграф, для которого данная матрица является матрицей смежности. Найдите матрицу инцидентности орграфа. |
|
Дано множество V = {1, 2, 3, 4, 5}. На этом множестве задано отношение f: х > у. Постройте орграф данного отношения. |
|
Даны графы G1 и G2, показанные на рис. 1.30.а, найти соединением G1 + G2. |
|
Для неориентированного графа, изображенного на рис. 5.14, постройте матрицу смежности и матрицу инцидентности. |
|
Для графа, изображенного на рис. 1.19 а), графы на рис. 1.19 б) и 1.19 в) являются остовными деревьями.. |
|
Для графа G = (A, U) найти матрицу смежности |
|
Для графа, изображенного на рис. 13, матрица C имеет вид: |
|
Для графов G1 = ({а1, а2, а3}; |
|
Дополнением графа G, изображенного на рис. 1.27, является граф G |
|
Задан граф G (V, E), где V = {v1, v2, v3, v4, v5}; Еv 1 = {v1, v3, v5}; 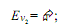 Е 3 v = {v1, v2, v5}; Е 3 v = {v1, v2, v5};Еv 4 = {v1}; Е 5 v = {v1, v2, v3, v4, v5}. 1. Задайте граф с помощью бинарного отношения, т. е. совокупности множества V и подмножества множества упорядоченных пар (vi, vj) ´ V×V. 2. Изобразите орграф. 3. Постройте матрицу смежности. |
|
Из графа G, показанного на рис. 1.27, добавлением вершины 5 образуется граф G1, добавлением дуги (3, 1) – граф G2, удалением дуги (3, 2) – граф G3, удалением вершины 2 – граф G4, отождествлением вершин 1 и 4 – граф G5, стягиванием дуги (2, 3) – граф G6 |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта