| Главная » Файлы » Математика » Нестандартные задачи по Математике |
Плоское дно фонтана описывается
| 25.10.2013, 23:23 | |
| Подсветка фонтана. Плоское дно фонтана описывается замкнутой ломаной линией без самопересечений, причем никакие три вершины ломаной не лежат на одной прямой. Для организации подсветки фонтана между двумя заданными углами (вершинами) по дну проложен гибкий натянутый кабель (см. рис.). Требуется написать программу, вычисляющую длину этого кабеля. 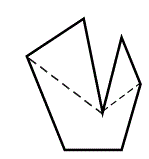 Исходные данные записаны в файле в следующей последовательности: в 1-ой строке — число вершин N (N £ 100); в каждой из последующих N строк — пара чисел через пробел, являющихся координатами вершин x1 y1 x2 y2 ¼ xN yN в порядке обхода ломаной против часовой стрелки, где 1, 2,..., N - номера вершин; в последней строке — номера соединяемых вершин k и l (1 £ k < l £ N). Координаты вершин являются вещественными числами. Результат вывести в виде числа. Результат проверяется с точностью до шести значащих цифр. Результирующее число может быть как с фиксированной точкой, так и в нормализованном виде. Решение.  Возможно несколько различных подходов к решению данной задачи. Один из них — поиск кратчайшего пути в графе , в матрице смежности которого записаны расстояния между вершинами границы фонтана, если их можно напрямую соединить шлангом и ¥, если этого сделать нельзя. Для построения такой матрицы необходимо уметь проверять наличие пересечения двух отрезков и в случае отсутствия пересечений — местоположение отрезка относительно границы фонтана (внутри или снаружи он находится). В последней подзадаче достаточно определить местонахождение одной из внутренних точек этого отрезка. | |
| Просмотров: 460 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта