| Главная » Файлы » Математика » Решение неравенств |
2sin2x - 3sinx - 2 < 0.
| 24.10.2013, 23:11 | |
| Решить неравенство 2sin2x - 3sinx - 2 < 0. Пусть sinx = t, где tє[-1; 1] (1), тогда получим квадратное неравенство
2t² - 3t - 2 < 0. Для его решения будем использовать свойства квадратной функции. 1) Её старший коэффициент равен 2. 2) D = 3² - 42(-2) = 9 + 16 = 25, следовательно, D > 0. 3) t1 = -0,5; t2 = 2, поэтому решением неравенства является множество чисел tє(-∞; - 0,5)(2; + ∞) (2). Пересечение множеств (1) и (2) есть множество [ - 1; -0,5). Произведем обратный переход к переменной х, получим неравенство. -1∞sinx < -0,5. Для решения этого двойного неравенства воспользуемся свойствами функции y = sinx. 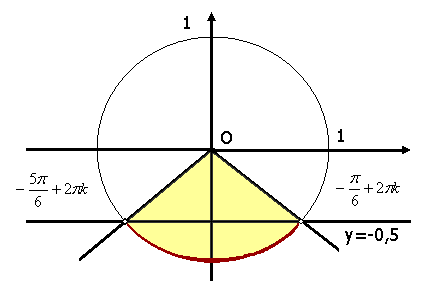 xє (5π/6- + 2πk; -π-6 + 2πk), где kєZ. Ответ: xє (5π/-6+ 2πk; -π/6 + 2k), где kєZ. | |
| Просмотров: 1728 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта