| Главная » Файлы » Математика » Решение неравенств |
√x + 1/x - 5 ≥ 0
| 25.10.2013, 02:25 | |
| Решить неравенство. √x + 1/x - 5 ≥ 0 Решение .x + 1 ≥ 0 x - 5 ≠ 0 ОДЗ: откуда имеем x є [-1; 5) U (5; +∞) Решим уравнение √x + 1/x - 5 ≥ 0 Числитель дроби равен 0 при x = -1, это и есть корень уравнения. Отметим найденный корень на чертеже (черным кружком, т.к. неравенство нестрогое), предварительно отметив ОДЗ: 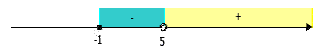 Чтобы определить знак на промежутке (-1; 5) возьмем число 0, ƒ (0)0 +√1/0 - 5 = 1/5 < 0 Чтобы определить знак на втором промежутке возьмем число 8, ƒ(8) = √8 + 1/8 -1 = 3/3 > 0 Точки 0 и 8 выбирались произвольно, но так, чтобы упростить процесс вычисления каждого значения функции. Ответ: ( - 5; + ∞). | |
| Просмотров: 421 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта