| Главная » Файлы » Математика » Решение неравенств |
√x +5 ≥ 7 - x.
| 25.10.2013, 02:40 | |
| Решить неравенство √x +5 ≥ 7 - x. Решение. При решении неравенств, содержащих квадратные корни, необходимо помнить, что возведение в квадрат обеих частей неравенства, сохраняя знак неравенства, можно лишь тогда, когда обе части неравенства принимают неотрицательные значения. Если же обе части неравенства принимают неположительные значения при возведении в квадрат необходимо изменить знак неравенства на противоположный. В перечисленных случаях возможны появления посторонних решений. Возведение неравенства в квадрат в тех случаях, кода части неравенства имеют противоположные знаки, т. е. одна часть принимает неотрицательные значения, а другая неположительные значения может привести к потере решений. Введем вспогательную переменную. Пусть t = √x + 5, где t 0 ≥, (из определения квадратного корня) тогда t² = x + 5; откуда x = t ² - 5 и имеем неравенство t ≥ 7 - t² + 5; t2 + t - 12 ≤ 0; ОДЗ: t є R. t² + t - 12 = 0; t1 = -4; t2 = 3. f(t) = t² + t - 12; эта функция непрерывна на всей области определения. Формулу, задающую функцию, удобнее записать так f(x) = (x - 3)(x + 4). f(4) =4² 2 + 4 - 12 = 8 >0; 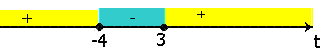 Таким образом, функция f(t) = t²2 + t - 12 принимает значения небольшие 0, если -4 ≤ t ≤ 3. Так как t ≥ 0, то 0 ≤ t4 ≤. Осуществим обратный переход к переменной x, тогда 03. Так как все части неравенства неотрицательны, то возведем их в квадрат 0 ≤x + 5 ≤ 9, откуда -5≤ x ≤4 и, следовательно, x є [-5; 3]. Ответ: x є [-5; 3]. | |
| Просмотров: 360 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта