| Главная » Файлы » Математика » Математика |
Для данного целого отличного от нуля числа b
| 30.10.2013, 22:40 | |
| Теорема Для данного целого отличного от нуля числа b , всякое целое число а единственным образом представимо в виде а = bq + r , где 0 ≤ r < | b |.. Доказательство Ясно, что одно представление числа а равенством а = bq + r мы получим, если возьмем bq равным наибольшему кратному числа b , не превосходящему а (см. рис. 1) ( a = 3b+r ) 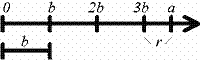 Рис. 1 Тогда, очевидно, 0 ≤ r < | b |. Докажем единственность такого представления. Ну пусть а = bq +r и а = bq 1 + r 1 — два таких представления. Значит 0 = а – а = b ( q – q 1 ) + ( r – r 1 ). Здесь 0 делится на b ; b ( q – q 1 ) делится на b , следовательно ( r – r 1 ) обязано делиться на b . Так как 0 ≤ r < b и 0 ≤ r 1 < b , то r – r 1 < b и r – r 1 делится на b , значит r – r 1 равно нулю, а, значит и q —q 1 равно нулю, т. е. два таких представления совпадают. | |
| Просмотров: 408 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта