Пусть α - произвольное число, s > 1, - Математика - Математика - Каталог файлов

Пусть α - произвольное число, s > 1,

	31.10.2013, 17:35
Пусть α - произвольное число, s > 1, а если при этом α = a / b - несократима, то s < n , где n таково, что Q n = b . Тогда неравенство 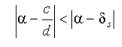возможно только если у несократимой дроби c / d знаменатель больше Q s . Доказательство. Мы знаем, что α всегда лежит между соседними подходящими дробями, поэтому всегда 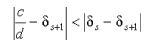Это неравенство проиллюстрировано рисунком 4, разглядывая который, нужно помнить, что 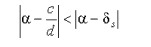(тогда иллюстрируемое неравенство становится очевидным, даже если c / d < δ_{s +1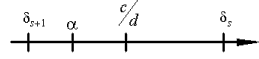} ). Рис. 4 Из проиллюстрированного неравенства следует, что 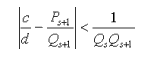и, если c / d ≠ δ _{s +1} , то 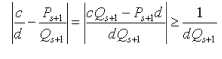Следовательно, 1/dQ _{s +1}<1/Q _s Q _{s +1} и, значит, d > Q s , что и требовалось. Если же c / d = δ _{s +1}, то d = Q _{s +1} > Q _{s .}
1 2 3 4 5 Категория: Математика \| Добавил: alexlat
Просмотров: 273 \| Загрузок: 0 \| Рейтинг: 0.0/0