| Главная » Файлы » Математика » Математика |
Пусть α ∈ R раскладывается в цепную дробь,
| 31.10.2013, 17:38 | |
| Пусть α ∈ R раскладывается в цепную дробь, например, с помощью процесса взятия целых частей и "переворачивания" дробных (этот процесс предложен в пункте 7 после формулировки основной теоремы о цепных дробях), т.е. 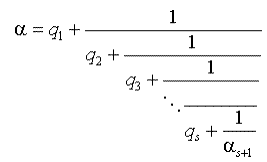 - результат очередного этапа процесса разложения. Тогда α лежит между δ s -1 и δ s , причем ближе к δ s , чем к δ s -1 . Доказательство. На ( s +1)-ом шаге разложения мы заменяем q s на q s + 1/ α s +1 , поэтому имеем точное равенство: α s +1 P s + P s -1 α = ----------------------------- α s +1 Q s + Q s -1 , значит α α s +1 Q s + α Q s -1 - α s +1 P s - P s -1 = 0. Преобразуем: α s +1 Q s(α -P s/Q s)+ Q s -1(α -/P s -1/Q s -1) = 0. Это равенство означает, что разности в скобках разных знаков. Кроме того, Q s > Q s -1 , α s +1> 1, значит |α -P s/Q s |< |α -P s -1/Q s -1 | | |
| Просмотров: 331 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта