| Главная » Файлы » Математика » Математика |
Пусть М - многоугольник на координатной плоскости
| 31.10.2013, 17:43 | |
| Пусть М - многоугольник на координатной плоскости с вершинами в целых точках, контур М сам себя не пересекает и не касается, S - площадь этого многоугольника, 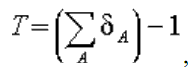 где суммирование ведется по всем целым точкам А , лежащим внутри и на границе этого многоугольника, причем δ A = 1, если точка А лежит внутри М , и δ A = 1/2, если точка А лежит на границе М . Тогда T = S . Доказательство этой леммы я здесь приводить не буду так как эта лемма, вообще говоря, не относится к теории чисел. Намечу только схему этого доказательства. 1) Для треугольника с вершинами в целых точках и без целых точек внутри утверждение очевидно. 2) Для выпуклого многоугольника - фиксируем одну из его вершин и соединяем ее прямыми с остальными вершинами - попадаем в случай треугольников. 3) Случай невыпуклого многоугольника рассматриваем как разность выпуклых многоугольников. | |
| Просмотров: 362 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта