| Главная » Файлы » Математика » Математика |
Разложим в цепную дробь число α = √ 2.
| 31.10.2013, 17:49 | |
| Разложим в цепную дробь число α = √ 2. Имеем q 1 = ⎣ √ 2 ⎦ = 1, β 1 = √ 2 - 1, т.е. α = 1 + ( √ 2 - 1). Далее, α 2 =1/β 1=1/√ 2 -1=√ 2 + 1/1= √ 2 + 1, q 2 = ⎣ √ 2 + 1 ⎦ = 2, β 2 = √ 2 - 1, α = 1 +1/2 +( √ 2 -1) Так как β 1 = β 2 , то нетрудно понять, что этот процесс зациклится и, если его не останавливать, то получится бесконечная цепная дробь: 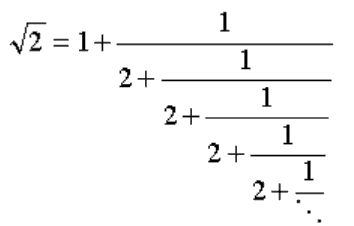 Все неполные частные в ней, начиная со второго, равны двойке. Очевидно, что если α ∈ R - иррационально, то описанный выше процесс бесконечен, так как иначе, в случае остановки этого процесса, α оказалось бы равным конечной цепной дроби, т.е. рациональному числу. Значит, всякое иррациональное число если и можно, то можно представить только бесконечной цепной дробью. Забудем пока про иррациональные числа и окунемся в приятный мир рациональных. Пусть α ∈ Q , α = a / b ; a , b ∈ Z , b > 0. Оказывается, что при этих условиях, указанный выше процесс разложения числа в цепную дробь всегда конечен и выполним с помощью достопочтенного и любимого нами алгоритма Евклида. Действительно, отдадим алгоритму числа a и b , и внимательно посмотрим, что получится. a = bq 1 + r 1 т.е. a/b= q 1 +1/b / r 1 b = r 1 q 2 + r 2 т.е. b/r 1 = q 2 +1/r 1 / r 2 r 1 = r 2 q 3 + r 3 т.е. r 1/r 2= q 3 +1/r 2 / r 3 . . . . . . . r n -2 = r n -1 q n + r n т.е. r n -2/r n -1= q n +1/r n -1 / r n r n -1 = r n q n +1 т.е. r n -1/r n= q n +1 . Значит:  где q 1 , q 2 ,..., q n +1 - как раз те самые неполные частные из алгоритма Евклида (вот откуда название этих чисел в цепных дробях). Таким образом, в случае рационального числа a / b , процесс разложения в цепную дробь конечен и дробь содержит не более b этажей. Наиболее одаренные читатели в этом месте уже поняли, что основная теорема о цепных дробях для рациональных чисел оказалась почти доказана (не доказали только единственность разложения, но она в случае конечных цепных дробей почти очевидна - приравняйте две цепных дроби и, рассуждая по индукции, получите, что у равных дробей совпадают все неполные частные). Согласитесь, что горизонтальные дробные линии в начертании цепной дроби сильно напоминают рисунок 3 из пункта 4 - отрезки, которые рисовали древние греки на песке, да и связь алгоритма Евклида с цепными дробями непосредственная и, можно сказать, даже трогательно-интимная. | |
| Просмотров: 714 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта