| Главная » Файлы » Математика |
| В разделе материалов: 3167 Показано материалов: 2741-2760 |
Страницы: « 1 2 ... 136 137 138 139 140 ... 158 159 » |
|
Пусть M и N – cередины оснований трапеции. Докажите, что если прямая MN образует равные углы с боковыми сторонами трапеции, то эта трапеция равнобочная. |
|
Пусть M и N – cередины оснований трапеции. Докажите, что если прямая MN образует равные углы с боковыми сторонами трапеции, то эта трапеция равнобочная. |
|
Пусть m и n—целые числа. Докажите, что mn(m+n) —четное число. |
|
Теорема (Ламэ, 1845 г.). Пусть n ∈ N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = Φ n +2 , b = Φ n +1 , где Φ k - k- ое число Фибоначчи. |
|
Геометрическое доказательство малой теоремы Ферма. Пусть p > 2— простое число. Сколько существует способов раскрасить вершины правильного p-угольника в a цветов? (Раскраски,которые можно совместить поворотом, считаются одинаковыми.) Получите формулу и выведите из нее малую теорему Ферма. |
|
Пусть p— простое число. Докажите, что любой простой делитель числа 2p − 1 имеет вид 2kp + 1. |
|
Пусть S = {4 k + 1 | k ∈ Z } - множество вот таких вот целых чисел. Легко проверить, что S замкнуто относительно умножения: |
|
Пусть x n = 2 n , где n пробегает N , - геометрическая прогрессия. |
|
Пусть x n = 2 n , где n пробегает N , - геометрическая прогрессия. Интуитивно ясно, что таких чисел в натуральном ряду мало, ибо чем "дальше в лес" по натуральному ряду, тем реже встречается степень двойки. Понятие плотности подтверждает это ощущение: |
|
Пусть x1 и x2 — действительные корни уравнения x2 – ax + a = 0, где a — действительное число. Найти такое значение a, чтобы величина выражения x²1 + x²2 была наименьшей. |
|
Пусть z1 и z2 —фиксированные точки комплексной плоскости. Дайте геометрическое описание множеств всех точек z, удовлетворяющих соотношениям: а) arg z − z1/z − z2 = 0; б) arg z1 − z/z − z2 = 0. |
|
Пусть α - произвольное число, s > 1, а если при этом α = a / b - несократима, то s < n , где n таково, что Q n = b . Тогда неравенство 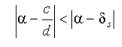 возможно только если у несократимой дроби c / d знаменатель больше Q s |
|
Пусть α - произвольное число, s > 1, а если при этом α = a / b - несократима, то s < n , где n таково, что Q n = b . Тогда неравенство 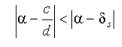 возможно только если у несократимой дроби c / d знаменатель больше Q s . |
|
Пусть α - произвольное число, s > 1, а если при этом α = a / b - несократима, то s < n , где n таково, что Q n = b . Тогда неравенство 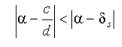 возможно только если у несократимой дроби c / d знаменатель больше Q s . |
|
теорема косинусов для трехгранного угла. Пусть α ,β ,γ – плоские углы трехгранного угла, A, B, C - противолежащие им двугранные углы. Тогда cosα = cosβ cosγ + sin β sinγ cos A. |
|
Пусть α ∈ R раскладывается в цепную дробь, например, с помощью процесса взятия целых частей и "переворачивания" дробных (этот процесс предложен в пункте 7 после формулировки основной теоремы о цепных дробях), т.е. |
|
Арифметико-геометрическое среднее Пусть α и b— два положительных числа, причем α > b. Построим по этим числам две последовательности {αn} и {bn} по правилам: α0 = α, b0 = b, αn+1 =αn + bn/2, bn+1 = √ αnbn (n ≥ 0). Докажите, что обе эти последовательности имеют один и тот же предел. Этот предел называется арифметико-геометрическим средним чисел α, b и обозначается μ(α, b). |
|
Пусть α, b, c—различные простые числа. Докажите, что числа √α,√b,√c не могут быть членами одной арифметической прогрессии.
Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа |
Просмотров: 291 |
Загрузок: 0 |
|
Дата: 26.10.2013
| Комментарии (0)
|
|
Пусть θ (1) = 1 и θ ( р α ) = 2 для всех р и α . |
|
Пусть Ω = {1, 2, 3, 4, 5, 6}— пространство элементарных исходов (например, при бросании игрального кубика). Следующие наборы подмножеств Ω являются α -алгебрами (доказать!): |
Категории раздела
| Математика [249] |
| Алгебра [136] |
| Геометрия [416] |
| Тригонометрия [109] |
| Задачи по теории вероятности [60] |
| Нестандартные задачи по Математике [232] |
| Задачи по комбинаторике [168] |
| Элементы математического анализа [51] |
| Смеси,Растворы , Сплавы.Проценты , Прогрессии ,Пропорции,Движение и работа [133] |
| Решение уравнений [190] |
| Функция и Графики [110] |
| Задачи на доказательство [151] |
| Задачи с параметрами [140] |
| Kоординаты и векторы [7] |
| Решение неравенств [229] |
| Разные решения одной задачи_ Одно решение разных задач [56] |
| Контрольные задачи по темам [12] |
| Формулы ,Таблицы, Правила, Теоремы [151] |
| Тесты [72] |
| Программирование [27] |
| Высшая Математика [77] |
| Теория графов [47] |
| Контрольные и самостоятельные работы пр Геометрии [344] |
Друзья сайта